My time as a grad student will soon draw to a close. With this comes the terrifying realisation that I’m going to start applying for jobs and, hopefully, interviewing soon, forever leaving my comfortable security blanket of academia.
With that horrible thought in mind, I’ve been doing some poking around to see what various kinds of technical interviews are like. Apparently, it is not entirely uncommon in such interviews to ask for solutions to little toy programming problems. These are viewed as a way of weeding out the hoi polloi, and as a way of determining how you approach a novel problem under stress.
One such problem that has been discussed at length is the fizzbuzz problem. The idea is simple:
Write a program that prints the numbers from 1 to 100. But for multiples of three print “Fizz” instead of the number and for the multiples of five print “Buzz”. For numbers which are multiples of both three and five print “FizzBuzz”.
Sounds simple enough, but if you’ve never though about this problem before, then I encourage you to do so before reading on. One way we might try to solve the problem is as follows:
# fizzbuzz with a loop
for (i in 1:100){
if (i%%3 == 0)
if (i%%5 == 0)
print("fizzbuzz")
else
print("fizz")
else
if (i%%5 == 0)
print("buzz")
else
print(i)
}
The above is very “C-ish” in spirit, or as Patrick Burns says in the R Inferno (which is necessary reading for anyone considering putting R on his/her resume) this is “speaking R with a C accent.” So we might want to think about vectorizing our code. My philosophy on vectorizing is that you win when it’s completely incomprehensible. Unfortunately, I don’t believe I’ve won here, but I did concoct this:
# vectorized fizzbuzz
m <- 1:100
m[which(m%%5==0)][which(m%%3==0)] <- "fizzbuzz"
m[which(as.numeric(m)%%3==0)] <- "fizz"
m[which(as.numeric(m)%%5==0)] <- "buzz"
print(m)
which will give you all kinds of warnings, but you can safely ignore them. These are just a few ways one can proceed. The problem has somewhat captivated internet nerds everywhere, with people coming up with solutions where no conditionals are used or trying to solve fizzbuzz with as few bytes of code as possible (which I first heard of through this R-bloggers blog). Why would anyone do this? One word: nerdcred.
Another toy problem I found while looking for job interview advice involves taking a fair 5-sided die and turning it into a fair 7-sided die. I originally found the question from a link pointing over to a stackoverflow page. The problem statement given there is
Given a function which produces a random integer in the range 1 to 5, write a function which produces a random integer in the range 1 to 7.
Since the problem does not explicitly say that the original function produces the numbers uniformly randomly, or that the new function should itself be under this restriction, there are several cute solutions you could concoct which fit the letter, though not the spirit of the problem. At that very stackoverflow page, user DrStalker gives this solution (with translation to R)
rand7 <- function() rand5()
which I think is my favorite such solution. My best friend (who otherwise wishes to remain nameless) gave this solution:
rand7 <- function() rand5() + floor(rand5() / 2)
which is more sneaky, since it is actually theoretically possible to generate all digits 1, 2, 3, 4, 5, 6, and 7 with this, though not uniformly. Again, if you haven’t thought about this problem before, give it a shot. In my opinion, it’s not all that trivial. What follows is the first solution I could come up with:
rand5 <- function() sample(1:5, 1) # the given
# Translate 5-sided die to fair coinflips
coin.flip <- function(){
n <- rand5()
if (n==1 || n==2)
return(0)
else
if (n==3 || n==4)
return(1)
else
coin.flip()
}
# Fair 7-sided die
rand7 <- function(){
x <- coin.flip() + coin.flip()*2 + coin.flip()*4
while (x == 0)
x <- coin.flip() + coin.flip()*2 + coin.flip()*4
return(x)
}
A few things about this solution before moving on. First, I think this has a kind of mathematical elegance, since it’s clear from this solution how to easily translate this solution into creating other fair dice. Second, it’s computationally inelegant in more ways than one. First of course, note that this could technically run forever. If you wanted to build your fair 7-sided die this way, you would probably want to do something about that, even if all you do is stop after “too many” tries. I didn’t do any such optimization because who the hell cares; that line of thought completely misses the point of the exercise. Lastly, both in terms of source code and in terms of actual running, the above solution is costly.
After satisfying myself in producing that solution, I decided to see what kinds of solutions others were coming up with. I’ve already mentioned what is, I think, my favorite solution. But there is a much more computationally elegant “real” solution provided by Adam Rosenfield (and translated into R):
rand7 <- function(.){
x <- rand5() + (rand5() - 1)*5
while (x > 21)
x <- rand5() + (rand5() - 1)*5
return(x%%7 + 1)
}
Now, it’s fairly obvious that these solutions are producing fair dice, assuming the original function is itself fair. However, suppose we wanted numerical verification. This is a good simple exercise in Monte Carlo simulation. And while we’re at it, let’s parallelize our simulation.
We’ll be using the built-in R library (as of 2.14) called parallel. This handy little guy merges the two former powerhouse parallel R libraries, namely multicore and snow. If you’re using Windows, then you have to use the snow side of parallel–which frankly, I find to be a huge, annoying mess. If you’re using a POSIX-like OS such as Linux or Mac OS X, then first pat yourself on the back for being awesome. Also, unlike the unwashed Windows peasants (only kidding!), you get your choice of multicore or snow functions. For the sake of inclusion, we’ll talk a bit about both approaches.
First, the snow way of doing things:
# The SNOW way of doing things -- necessary for Windows users
library(parallel)
# Setting up the workers. The function detectCores() used below is a
# function from library(parallel) which finds the total number of
# available cores. You can change the call below to a smaller number
# if you don't want to use all of your cores for some reason.
cl <- makeCluster(detectCores())
# Send our functions to the workers
clusterEvalQ(cl, rand5 <- function() sample(1:5, 1))
clusterEvalQ(cl,
coin.flip <- function(.){
n <- rand5()
if (n==1 || n==2) return(0) else
if (n==3 || n==4) return(1) else
coin.flip()
}
)
# Our many die rolls, stored as a list
results <- parSapply(cl=cl, 1:1e5, rand7)
table(unlist(results))
which gives output
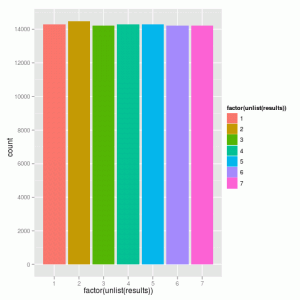
1 2 3 4 5 6 7
14360 14344 13990 14447 14352 14133 14374
Which looks exactly like we had hoped it would. We can also look at a quick summary
summary(unlist(results))
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1 2 4 4 6 7
We can also flex our mighty R muscles and give a pretty histogram using Hadley Wickham’s incredible ggplot2 package
 {.alignnone
.size-medium .wp-image-468 width=”300”
height=”300”}
{.alignnone
.size-medium .wp-image-468 width=”300”
height=”300”}
which looks exactly like we expect it to.
Ok, so that’s the snow way of doing things; now for my personal favorite, the multicore way of doing things. The function we will be using is mclapply, which is exactly what it looks like. It’s a multicorelapply function.
library(parallel)
results <- mclapply(X=1:1e5, FUN=rand7, mc.cores=detectCores())
table(unlist(results))
Note the difference. And for those who think I’m just being cranky for no good reason, here’s a little speed test
time.capply <- system.time({results <- parSapply(cl=cl, 1:1e5, rand7)})[3]
time.capplylb <- system.time({results <- parSapplyLB(cl=cl, 1:1e5, rand7)})[3]
time.mclapply <- system.time({results <- mclapply(X=1:1e5, FUN=rand7, mc.cores=detectCores())})[3]
cat(sprintf("With %d cores, the times are:
clusterApply():\t%.3f seconds
clusterApplyLB()\t%.3f seconds
mclapply():\t\t%.3f seconds
", detectCores(), time.capply, time.capplylb, time.mclapply))
which gives output
With 4 cores, the times are:
clusterApply(): 0.502 seconds
clusterApplyLB() 0.492 seconds
mclapply(): 0.416 seconds
Again, note the difference.
Finally, it is worth mentioning that there is another way we could parallelize things, namely by using the foreach package. I’m not a huge fan of foreach, but you might find it useful depending on what you are trying to do.
As for more “toy” problems, the motherload is over at Project Euler. These problems hastily go from being a fun, simple way to practice R to being fairly cumbersome and challenging. I’ve posted several Project Euler in R solutions on this blog, and I have a bunch more that I’m too lazy to write up and post. Should you get bitten by the Project Euler bug, once you get an initial solution to a problem there, try your best to get the run time to below a minute (or below a second). This can sometimes be a deeply frustrating (given how R performs on loops), though ultimately rewarding process. Have a look.